Příklady BB01 - Fyzika, Doc. Schauer
- Časový rozdíl mezi spatřením nebezpečí na vozovce a sešlápnutím brzdového
pedálu je u průměrného řidiče asi 0,6 s. Automobil může brzdit s maximálním
zpožděním
5 m.s-2 . Vypočtěte celkovou délku dráhy, kterou vozidlo urazí od okamžiku, kdy řidič spatřil nebezpečí až do úplného zastavení. Předpokládejte, že jeho rychlost je 60 km/h. [37,8 m] - Sedačka kolotoče se pohybuje rovnoměrným pohybem po kružnici o poloměru 5,2 m. Oběžná doba sedačky je 5 sekund. Vypočtěte: a) velikost rychlosti sedačky, b) velikost dostředivého zrychlení sedačky, c) úhel, o který je odkloněn závěs sedačky od svislého směru. [6,53 m.s-1, 8,20 m.s-2, 39,7o]
- Kulička zavěšená na niti se pohybuje rovnoměrným pohybem po vodorovné kružnici o poloměru 25 cm a vykonává půl otáčky za sekundu. Vypočtěte: a) velikost dostředivého zrychlení kuličky, b) úhel, o který je odkloněn závěs kuličky od svislého směru. [2,46 m.s-2, 14o]
- Těleso o hmotnosti 0,8 kg je vrženo svisle vzhůru. Při svém pohybu má ve
výšce 10 metrů kinetickou energii 20 J, gravitační zrychlení je
9,81 m.s-2 . a) Jakou má těleso v uvedené výšce potenciální energii? b) Jaké maximální výšky toto těleso dosáhne? c) Jakou rychlostí bylo těleso vrženo? d) Jakou mělo těleso rychlost ve výšce 10 m? [78,48 J, 12,5 m, 7,07 m.s‑1] - Závodník vrhl oštěp do vzdálenosti 65 m. Let oštěpu trval 3,2 s. Určete jakou rychlostí a pod jakým elevačním úhlem byl oštěp vymrštěn. K odporu vzduchu nepřihlížíme a předpokládáme, že oštěp byl vymrštěn z povrchu Země. [25,7 m.s-1, 37,7o]
- Atlet vrhl oštěp do vzdálenosti 65 m pod úhlem 38 o. Jak dlouho trval let oštěpu a jakou počáteční rychlostí byl oštěp vržen? K odporu vzduchu nepřihlížíme a předpokládáme, že oštěp byl vymrštěn z povrchu Země. [3,29 s, 25,6 m.s-1]
- Pod jakým elevačním úhlem se musí vrhnout těleso, aby se výška výstupu právě rovnala vzdálenosti dopadu? [76o]
- Pod jakým úhlem od vodorovné roviny musíme vrhnout těleso počáteční rychlostí
28 m.s-1 , aby těleso vystoupilo do maximální výšky 30 m? [60o] - Pod jakým úhlem od vodorovné roviny musíme vrhnout těleso počáteční rychlostí
28 m.s-1 , aby těleso doletělo do vzdálenosti 30 m? [11o] - Pod jakým elevačním úhlem se musí vrhnout těleso, aby výška výstupu byla dvakrát větší než vzdálenost dopadu? [83o]
- Z děla umístěného na pobřeží 30 m nad hladinou moře je vystřelena střela
pod úhlem 45o od vodorovné roviny s počáteční rychlostí
1000 m.s-1 . Jaká je vodorovná vzdálenost místa na hladině moře, kde střela zasáhne svůj cíl? Odpor vzduchu zanedbejte. [101,8 km] - Tenisový míček je odpálený vodorovným směrem ve výšce 120 cm nad zemí rychlostí
42 m.s-1,
(g = 9,81 m.s-2) . Vypočítejte: a) dobu trvání letu míčku, než dopadne na zem, b) vzdálenost dopadu míčku od hráče. [0,5 s, 20,8 m] - Kámen vržený rychlostí v0 = 12 m/s pod úhlem 45o od vodorovné roviny, dopadl na zem ve vzdálenosti x od místa vrhu. Z jaké výšky by bylo nutno tentýž kámen hodit ve vodorovném směru stejnou rychlostí v0 = 12 m/s, aby dopadl na totéž místo. [7,4 m]
- Kámen vržený vodorovně z výšky h = 6 m počáteční rychlostí v0 = 12 m/s dopadl na zem ve vzdálenosti x od místa vrhu. Pod jakým úhlem od vodorovné roviny bychom museli vrhnout kámen stejnou rychlostí v0 = 12 m/s ze země, aby dopadl na totéž místo. [32,4o]
- Příklad k procvičení (nebude u písemek)
Žebřík dlouhý 7,6 m je opřen o svislou dokonale hladkou stěnu. Hmotnost žebříku je 40 kg a těžiště je v jeho geometrickém středu. Součinitel statického tření mezi žebříkem a podlahou je 0,4. Vypočtěte: a) nejmenší úhel, který může žebřík svírat s podlahou aby žebřík neuklouzl,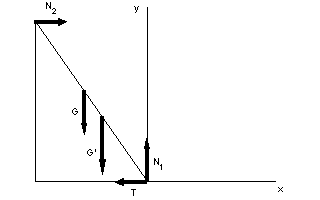
Obrázek k příkladu "žebřík" b) je-li dolní konec vzdálen od stěny 4,5 m, jak vysoko může po žebříku bezpečně vystoupit osoba o hmotnosti 90 kg? [51o18', 4,28 m] -
Za jak dlouho ujede vozík na nakloněné rovině dráhu s = 45 m? Vozík je spojen se závažím hmotnosti 100 kg visícím přes kladku (podle obrázku). Hmotnost vozíku je 500 kg, sklon nakloněné roviny je 30o. Vozík se rozjíždí z klidu. [6,06 s]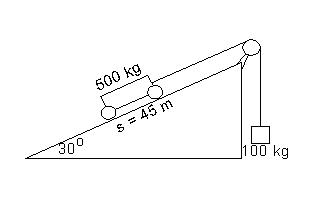
Obrázek k příkladu "vozík s kladkou" - Za jak dlouho dosáhne vozík na nakloněné rovině rychlosti 10 km/h? Vozík je spojen se závažím hmotnosti 100 kg visícím přes kladku (podle předchozího obrázku). Hmotnost vozíku je 500 kg, sklon nakloněné roviny je 30o. Vozík se rozjíždí z klidu. [1,13 s]
- Železná kulička hmotnosti 0,1 kg upevněná na niti délky 0,5 m se rovnoměrně pohybuje po vodorovné kružnici. Niť přitom opisuje plášť kužele a svírá se svislým směrem úhel 30o. Určete a) dostředivou sílu a b) dobu oběhu kuličky. [0,566 N, 1,32 s]
- Střela o hmotnosti 5 g byla vystřelena vodorovně do kostky hmotnosti 3 kg, která leží na vodorovné rovině. Součinitel smykového tření mezi kostkou a rovinou je 0,2. Střela uvízla v kostce a kostka se posunula o 25 cm. Jaká byla rychlost střely? [595 m.s-1]
- Kvádr sklouzl po nakloněné rovině dlouhé 5 m rovnoměrně zrychleným pohybem
za 2 s. Určete součinitel smykového tření kvádru,
svírá-li nakloněná rovina s vodorovnou úhel 30o. (Rovnici určující součinitel tření odvoďte!) [0,283] - Kvádr sklouzl dolů po nakloněné rovině dlouhé 5 m rovnoměrně zrychleným pohybem za 2,5 s. Součinitel smykového tření kvádru byl 0,35. Určete úhel sklonu nakloněné roviny vzhledem k vodorovné rovině. [28,1o]
-
Zatáčka o poloměru 30 m byla upravena skloněním povrchu vozovky o úhel
15 o. Jak se tím zvýšila maximální bezpečně průjezdná rychlost
vozidel,
je-li součinitel tření pneumatik na vozovce 0,7? [67,7 km/h] - Zatáčka o poloměru 35 m byla upravena skloněním povrchu vozovky. O jaký
úhel je třeba vozovku naklonit, aby se zvýšila maximální bezpečně průjezdná
rychlost vozidel na 80 km/h,
je-li součinitel tření pneumatik o vozovku 0,6 ? [24,2o] - Za jakou dobu proběhne vozík o hmotnosti 1 t délku dráhy 45 m po nakloněné
rovině s úhlem sklonu 20o,
je-li součinitel vlečného tření 0,2? Jaké bude jeho zrychlení? [7,71 s] - Po nakloněné rovině délky 75 m s úhlem sklonu 32o od vodorovné roviny se valí homogenní válec bez klouzání. Určete zrychlení a závislost proběhnuté dráhy jeho těžiště na čase. [3,47 m.s-2, s=1,74.t2]
- Po nakloněné rovině s úhlem sklonu 17o od vodorovné roviny jede
samospádem vozík o hmotnosti 300 kg. Vozík má 4 stejná kola. Vypočítejte moment
setrvačnosti jednoho kola, jehož poloměr je 30 cm. Na konci nakloněné roviny
dlouhé 100 m vozík dosáhne rychlosti
15 m.s-1. Nápověda: kinetická energie vozíku je součet translační kinetické energie vozíku a rotační kinetické energie kol. [10,45 kg.m] - Po nakloněné rovině se valí dolů homogenní koule. Koule vykoná jednu otáčku za 2 s. Poloměr koule je 30 cm a její hmotnost 5 kg. Vypočítejte kinetickou energii koule. [3,11 J]
- Po nakloněné rovině se valí válec. Vypočítejte úhel sklonu nakloněné roviny
víte-li , že na začátku nakloněné roviny byl válec v klidu a na konci nakloněné roviny dlouhé 25 m dosáhne válec rychlosti15 m.s-1. [43,5o] - Po nakloněné rovině délky 125 m s úhlem sklonu 25o od vodorovné
roviny se valí homogenní koule (d = 68 cm,
r = 2500 kg m-3). Určete dráhu, kterou urazí jeho těžiště za 5 s,byla-li počáteční rychlost nulová. [37 m] - Po nakloněné rovině s úhlem sklonu 30o se valí tenká obruč. Vypočítejte velikost zrychlení s jakým se pohybuje těžiště obruče. [2,45 m.s-2]
- Po nakloněné rovině s úhlem sklonu 35o se valí koule. Vypočítejte velikost zrychlení s jakým se pohybuje těžiště koule a rychlost na konci nakloněné roviny dlouhé 12 m. [4,02 m.s-2, 9,82 m.s-1]
- Po nakloněné rovině se valí tenká obruč se zrychlením těžiště
a = 3 m.s-1. Vypočítejte úhel sklonu nakloněné roviny. [37,7o] - Příklad k procvičení (nebude u písemek)
- Stacionární umělá družice Země je těleso, které lze pozorovat stále na stejném místě oblohy vzhledem k pozorovateli. Za předpokladu, že družice obíhá v rovině rovníku vypočítejte: a) úhlovou rychlost stacionární družice, b) její oběžnou rychlost, c) její výšku nad povrchem Země. Poloměr Země je 6378 km. [35,9.103 km, 7,27.10-5 s-1, 3,07 km/s]
- Vypočítejte kinetickou energii tělesa o hmotnosti 9,2 tun , které dopadlo na Zem z velké výšky h >> R, kde R=6378 km je poloměr Země. [5,76.1011 J]
- Vypočítejte kinetickou energii tělesa o hmotnosti 5 tun, které dopadlo
na Zem z výšky 65000 km,
je-li poloměr Země 6378 km a hmotnost Země 5,98.1024 kg. [2,85.1011 J] - Vypočítejte hmotnost Slunce,
předpokládáme-li , že Země kolem něj oběhne za 1 rok po kruhové dráze o poloměru 149,5 milionů km. [1,98.1030 kg] - Hmotný objekt tvaru pravidelného hranolu plave na vodě.
Naložíme-li na něj náklad 500 kg, ponoří se o 1 cm hlouběji. Jak velká je plocha jeho dna? [50 m2] - Jak velká tlaková síla spodní vody působí na svislou obdélníkovou stěnu
základové betonové vany, jejíž šířka je 12 m, výška 4,4 m,
je-li vana zatopena do poloviny své výšky spodní vodou? - Jak velká tlaková síla vody působí na svislou obdélníkovou hráz, jejíž
šířka je 25 m, výška 15 m,
je-li hráz zatopena do 2/3 své výšky vodou? [12,3 MN] - Určete výslednou tlakovou sílu vody na hráz údolní přehrady mající tvar lichoběžníka. Šířka hladiny je a=80 m, spodní základna b=52 m a výška hladiny nad dnem c=22 m. [146 MN]
-
- Dřevěná konstrukce o hmotnosti 600 kg má být potopena pod vodou zatížením
kameny. Určete minimální hmotnost kamenů,
je-li hustota dřeva650 kg.m-3 a hustota kamene2500 kg.m-3. [323 kg] - Jaká je plocha nejmenší ledové kry 30 cm silné, která právě unese člověka
vážícího 90 kg. Hustota ledu je
917 kg.m-3. - Nádoba naplněná vodou má ve výšce 15 cm nad vodorovnou rovinou otvor z
něhož vodorovně vytéká voda a dopadá na vodorovnou rovinu ve vzdálenosti 20 cm
od nádoby. Určete jakou rychlostí voda vytéká.
[1,14 m.s-1]
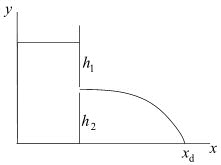
Obrázek k příkladům "nádoba" - Nádoba naplněná vodou má ve výšce 30 cm nad vodorovnou rovinou otvor z něhož vodorovně vytéká voda a dopadá na vodorovnou rovinu. Otvor je 15 cm pod hladinou. Určete vzdálenost místa dopadu vody od nádoby. [42,4 cm]
- Nádoba naplněná vodou má ve výšce 15 cm nade dnem otvor, z něhož vodorovně vytéká voda.Vod a dopadá na vodorovnou rovinu, na které stojí nádoba, ve vzdálenosti 20 cm od nádoby. Určete v jaké výšce ode dna je hladina vody v nádobě. [21,7 cm]
- Do nádoby přitéká voda s konstantním objemovým tokem. Za jednu sekundu přiteče 150 cm3 vody. Na dně nádoby je otvor s průřezem S = 0,5 cm2. V jaké výšce se ustálí voda v nádobě, když zanedbáme tření u výtoku?
- Jaký tlak musí být ve vodorovném potrubí položeném 2 m pod zemí,
má-li voda vystoupit do nejvyššího patra domu 30 m nad zemí a ještě vytékat rychlostí3 m.s-1. Ztráty v potrubí zanedbejte! Rychlost v hlavním potrubí je2 m.s-1. Jak vysoko nad zemí musí být vodárenská nádrž? [416 kPa, 30,5 m] - Pružina zatížená silou 5 N se prodlouží o 5 cm. Jaká je celková energie kmitavého pohybu,jestliže bude na této pružině kmitat těleso s amplitudou výchylky 2 cm? [0,02 J]
- Závaží o hmotnosti 5 kg zavěšené na pružině ji prodlouží o 122 mm. Místo
něj pak zavěsíme na tutéž pružinu závaží o hmotnosti 1 kg a tuto soustavu
rozkmitáme. Určete: a) dobu kmitu netlumených oscilací, b) logaritmický
dekrement tlumení,
je-li součinitel tlumení6,8 s-1, c) frekvenci tlumených kmitů pro případ b) . [0,313 s, 2,27, 3,00] - Bod o hmotnosti 5 kg kmitá harmonickým netlumeným pohybem o frekvenci 0,5 Hz s amplitudou kmitů 3 cm. Určete rychlost, zrychlení a sílu působící na oscilátor v okamžiku kdy má výchylku 1,5 cm! [0,082 m.s-1, 0,148 m.s -2, 0,74 N]
- Celková energie kmitajícího tělesa je 0,96 mJ. Maximální síla působící na těleso je 0,48 N a perioda kmitů je 0,3 s. Určete: a) hmotnost tělesa, b) amplitudu výchylky. Počáteční fáze je 60o. [273 g, 4 mm ]
- Potenciálmí energie kmitajícího tělesa při výchylce 3 cm je 0,96 mJ. Maximální síla působící na těleso je 0,48 N a perioda kmitů je 0,2 s. Určete: a) amplitudu výchylky, b) hmotnost tělesa. [22,5 cm, 2,16 g]
- Na misku o hmotnosti 0,5 kg zavěšenou na pružině o tuhosti
250 N.m-1 dopadlo z výšky 30 cm závaží hmotnosti 280 g a zůstalo ležet na misce. Miska začala kmitat. Určete amplitudu netlumených kmitů misky. - Logaritmický dekrement tlumení kyvadla je roven 0,01. Vypočítejte, kolikrát se zmenší amplituda kmitů po 100 kmitech.
- Harmonický oscilátor kmitá s počáteční amplitudou výchylky 30 cm a logaritmickým dekrementem tlumení 0,02. Určete amplitudu výchylky kmitů po 50 kmitech. [11 cm]
- Jaký je logaritmický dekrement tlumení oscilátoru, který kmitá s kmitočtem
2 Hz,
je-li jeho počáteční amplituda výchylky 5 cm a tato amplituda klesne za 5 minut na 0,5 cm? [3,84.10-3] - Vypočítejte součinitel tlumení kmitů,
je-li podíl dvou po sobě jdoucích maximálních výchylek na tutéž stranu roven 2 a perioda tlumených kmitů je 0,5 s. Jaká by byla perioda netlumených kmitů za stejných podmínek? [1,39, 0,499 s] - Vypočítejte součinitel tlumení kmitů,
je-li podíl dvou po sobě jdoucích maximálních výchylek (ležících vzájemně na opačných stranách) roven 2 a perioda tlumených kmitů je 0,2 s. Jaká by byla perioda netlumených kmitů za stejných podmínek? [6,93, 0,195 s] - Stanovte dobu, při které dojde k maximální výchylce při tlumených kmitech,
které jsou dány rovnicí výchylky
x = x0e-dtsin ( wt) - Frekvence tlumených kmitů je 2,5 Hz, součinitel tlumení je
2 s-1 a počáteční fáze je p/4. Stanovte čas, pro který bude výchylka tlumených kmitů maximální. - Pozorováním tlumeného pohybu bylo zjištěno, že po dvou po sobě jdoucích výchylkách na stejnou stranu se amplituda kmitů zmenšila o 6/10 a že perioda tlumených kmitů je 0,5 s. Určete součinitel tlumení a frekvenci netlumených kmitů, které by probíhaly za stejných podmínek.
- Perioda netlumeného kmitavého pohybu je 80 ms. Určete, zda je tato soustava
tlumena podkriticky, kriticky nebo nadkriticky,
je-li součinitel tlumených kmitů50 s-1.
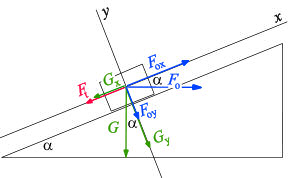 |
Obrázek k příkladům "zatáčka" |
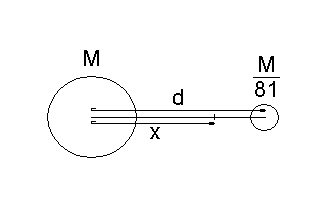
Ve kterém bodě na spojnici Země a Měsíce je výsledná intenzita gravitačního pole Země nulová? Hmotnost měsíce je rovna 1/81 hmotnosti Země, vzdálenost středů planet je 384.103 km. [338.103 km]
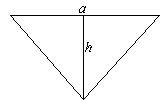
Určete výslednou tlakovou sílu vody na stěnu tvaru rovnoramenného trojúhelníka znázorněnou na obrázku,